Quadratic Functions

This is how to identify Quadratic Functions:
The standard Form is: ax² + bx + cy² + dy + e= 0

Circle Equation- A=C
So for example X²+Y²=9. So the center is at the origin. And the radius is 3.

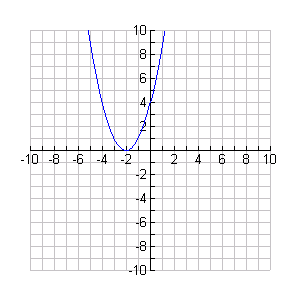
Parabola- A or C = 0
For example: X²+4X+4. So the intercepts are at 2 on the x axis and 4 on the y.

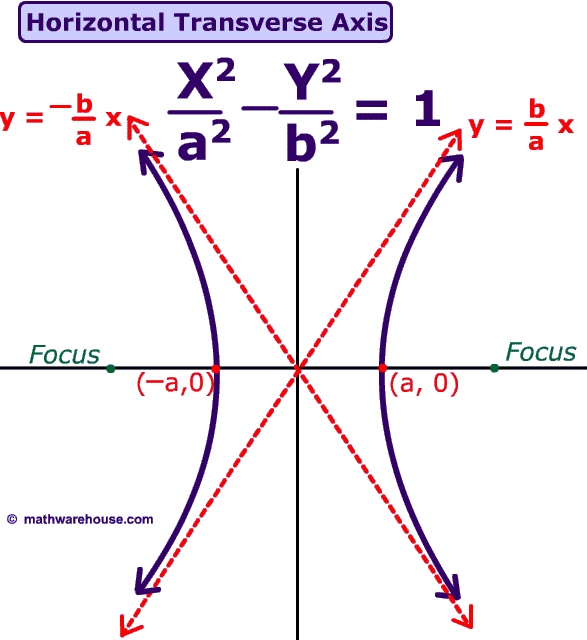
Hyperbola- A or C has different signs from each other
For example: (X²/A²) - (Y²/B²) = 1
The two red lines are asymptotes. Or lines the hyperbola will continue to try to reach but will never reach.



Ellipse- A is not equal to C. However the signs are still the same.
For example: x²/16 + y²/4 = 1

Multiplying Matrices

Scalar matrix multiplications
Distribute the outside number for all the numbers on the inside.

When multiplying matrices. We must note that the dimensions are to be similar. The colums of the 1st matrix and the rows of the 2nd matrix must be equal. Then use the outer dimensions as the product matrix. So...
If we multiply a 2×3 matrix with a 3×1 matrix, the product matrix is 2×1

Here is how we get M₁₁ and M₂₂ in the product.

M₁₁ = r₁₁× t₁₁  +  r₁₂× t₂₁  +   r₁₃×t₃₁
M₁₂

 

 

Dimensions of a matrix

When identifying the dimensions of a matrix. One must always follow the rule. Row Times column.
For example if there are 4 rows and 5 columns. The dimensions of the matrix would be.
4 X 5.

Ex: There are 2 rows and 4 columns. Therefore the dimensions of the matrix would be 2 x 4.

*Be carefull that you don't go columns by rows. Many people mess up like this.

The rule is : Rows x Columns

Error Analysis - Systems of Equations + How to graph equations.

Many times while doing systems of equations people have common errors in their calculation.

Example :
Equation : Y= 2x+4
Y= 5x-1

Many people make this mistake. When graphing we must consider three things of the Y= MX+B equation.
B is the vertical shift in which we shift the parent graph to our equation. If B were 4 we are to shift up 4. In which the person doing this graph only shifted up 3. That is the mistake. To completely graph the equation Y=2x + 4. First we must go up 4 on the y axis. Then due to the slope being 2. We must follow the slope rule, Rise over run, Therefore we go up 2 and over 1.

And for the second equation the same rule applies.  Y= 5X-1. The graph would shift down one. Then it would strech due to the slope being 5/1. Remember that slope is rise over run. Therefore you go up 5 and over one to get your second point after shifting down 1.

Examples of Solving Systems of Equations

1. This is your first equation.

2. This is your second equation.

You will be using these equations to substitute each equation into the other. Hence Substitution method.

3. This is the equation you will be using to make it equal to Y.

4. To make the equation equal to Y. In this equation you would move the x over hence subtracting it from ten. Making the equation Y = 10-x

5. This is the equation you will be inserting Y= 10-x into.

6. Making the resulting equation 2x+(10-x) = 15

7. Simplify the equation to make it equal X + 10 = 15

8. Once you simplify the equation all the way it will equal. X = 5.

9.Insert the 5 into one of the equations to find out what y is.

10. This makes the equation 5+Y=10

11. This makes Y = 5 also.

12. put the points together to sum them up to (5,5)

That is your answer.

*When substituting make it easier on yourself and choose the easier equation to find your first variable.

Solving a System of Linear Equations in Two Variables